Welcome to RepLAB!¶

Current version: 1.0.1 (GitHub / latest release ZIP / installation instructions).

RepLAB provides tools to study representations of finite groups and decompose them numerically. It is compatible with both MATLAB and Octave.

Key features¶

Provable decompositions	Modular construction	Optimization toolbox integration	Interactive documentation	Open source


RepLAB’s numerical decomposition into irreps can be certified	Construct new groups and representations by simple combination	Solves convex optimization problems with symmetries efficiently	Extensive documentation accessible by a click	Full open source software compatible with the GNU/Octave interpreter

RepLAB in action¶

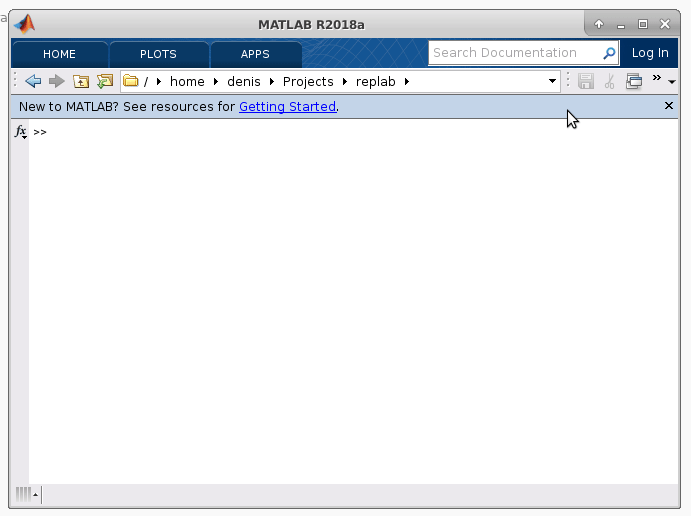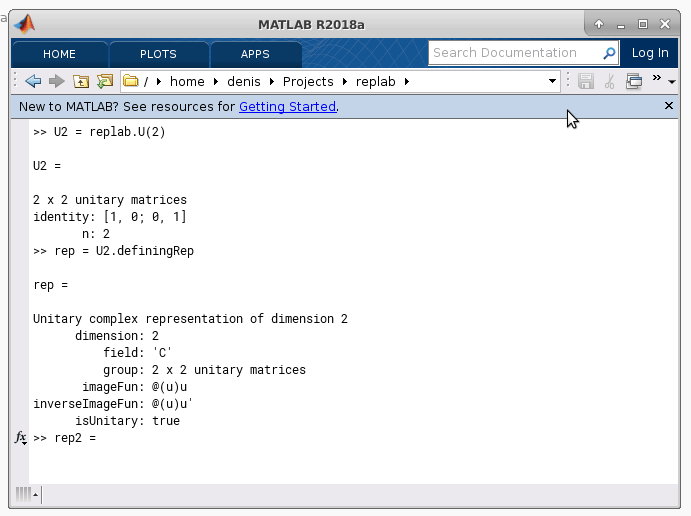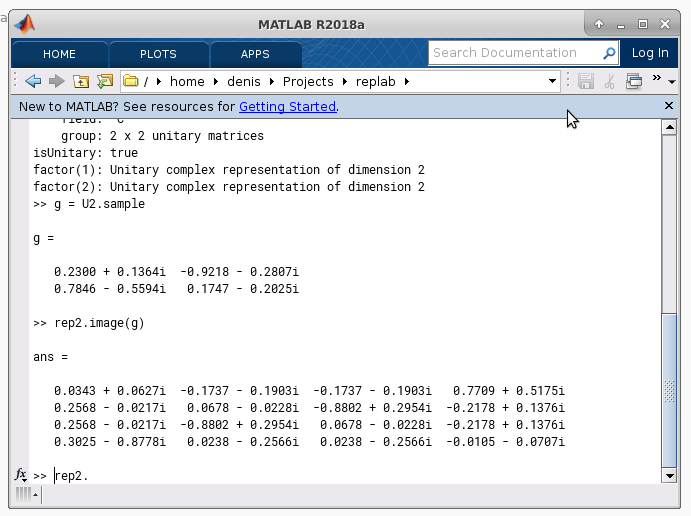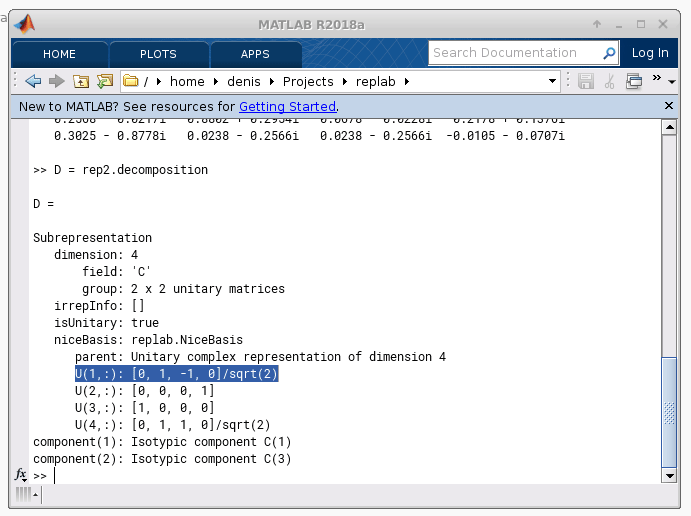
_images/CompactGroups.gif — Decomposition of the \(U \otimes U\) representation of the unitary group of dimension 2.¶

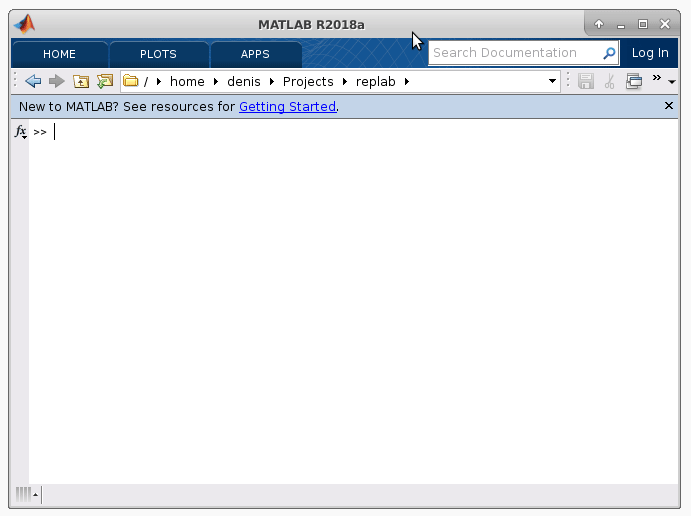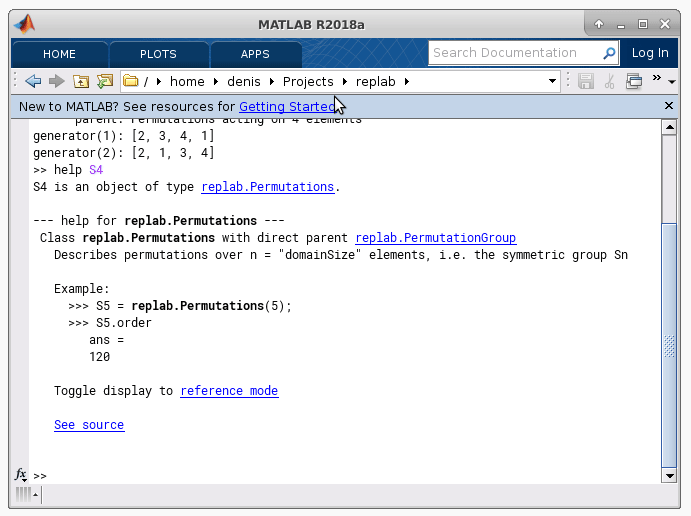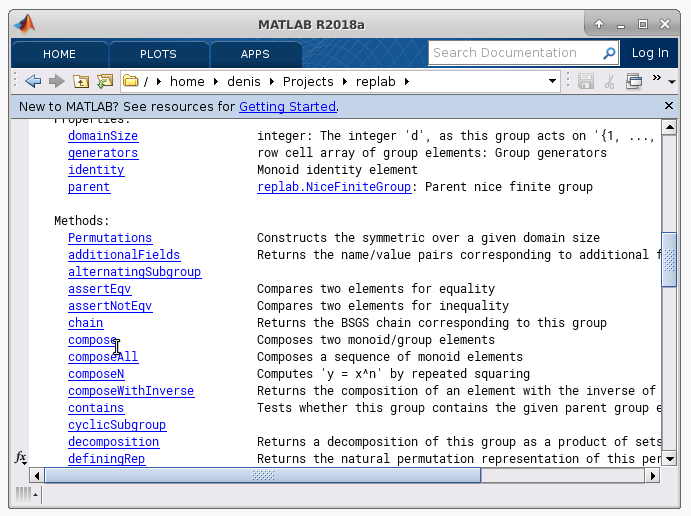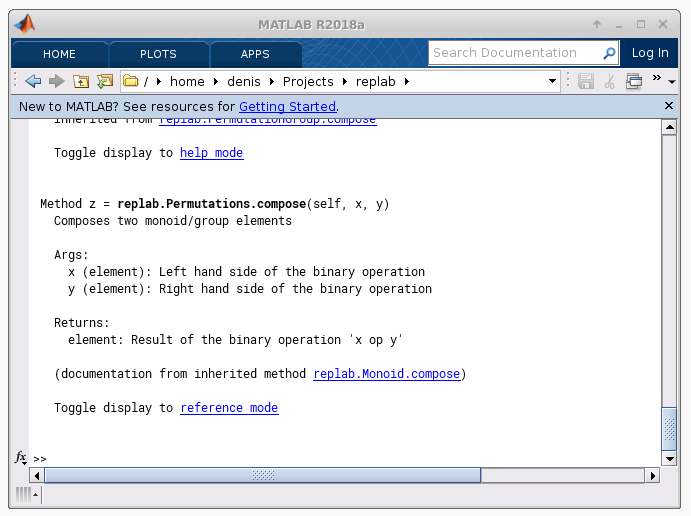
_images/HelpSystem.gif — Integrated help system in RepLAB¶

How to start using RepLAB?¶

Have a look at the tutorials! They have everything to get you started, from installation instructions to hands-on examples.

The documentation of RepLAB is organized along 4 directions, following this approach:

Tutorials: are short hands-on presentations that give you a taste of the goodness of RepLAB
How-to guides: are concise recipes showing how to achieve a specific goal
Topic guides: are understanding-oriented presentations explaining the big picture and key notions on which this software is built
Technical reference: contains a complete and accurate description of each object of the library

Work in progress¶

RepLAB is a work-in-progress. In particular:

We are still working on the estimation/control of numerical errors (a few criteria are currently hard-coded). That said, RepLAB works fine for representations of medium size (\(d\) equal to a few thousands).
While RepLAB implements several computational group theory algorithms, their performance is not competitive with dedicated computational group theory software such as GAP or Magma.
The documentation is still a work in progress, and tutorials/how to guides/… will be added as the project progresses.

Why RepLAB?¶

Because no open source library decomposes arbitrary permutation/monomial representations into irreducible representations over the reals. RepLAB implements numerical methods that perform this decomposition up to machine precision.

That said, other libraries working on the same problem space include:

The GAP System 4 package RepnDecomp by Kaashif Hymabaccus.
The GAP System 3 package AREP by Sebastian Egner and Markus Püschel.
NCSOStools includes an implementation of the Murota-Kanno-Kojima-Kojima-Maehara algorithm to decompose matrix *-algebras.

Additional features unique to RepLAB:

RepLAB follows a category-based approach. This enables preserving the structure of objects under operations, naturally allowing composition of finite and continuous groups/representations together for instance.
RepLAB integrates with the convex optimization framework YALMIP. This allows to formulate optimizations subject to symmetries easily.

Contributors¶

RepLAB and the group theory/linear algebra libraries it depends on were initiated by Denis Rosset and Jean-Daniel Bancal. The project now has more contributors.

RepLAB references in the /external directory the following libraries: the MOxUnit test framework by Nikolaas N. Oosterhof, the YALMIP toolbox for optimization modeling by Johan Löfberg, the SDPT3 solver, and the VPI big integer library by John D’Errico.

Feedback and suggestions are always welcome. We ask participants to follow the guidelines of the Typelevel Code of Conduct.

Recent Blog Posts